笛卡尔符号法则

• 正方向：光线由左向右传播为正。
• 线量规定：以光学元件顶点为原点，左负右正，下负上正。
• 角量规定：从法线或光轴算起，按小于90°方向旋转，顺时针为正，逆时针为负。 其中光轴与法线夹角从光轴转到法线。
• 单个字母表示的量有正负，符合上述符号法则。图中标记的量冠正符号后，均非负。代入具体数据时，用数据替换相应单个字母，且数据应符合上述符号法则。

阿贝不变式

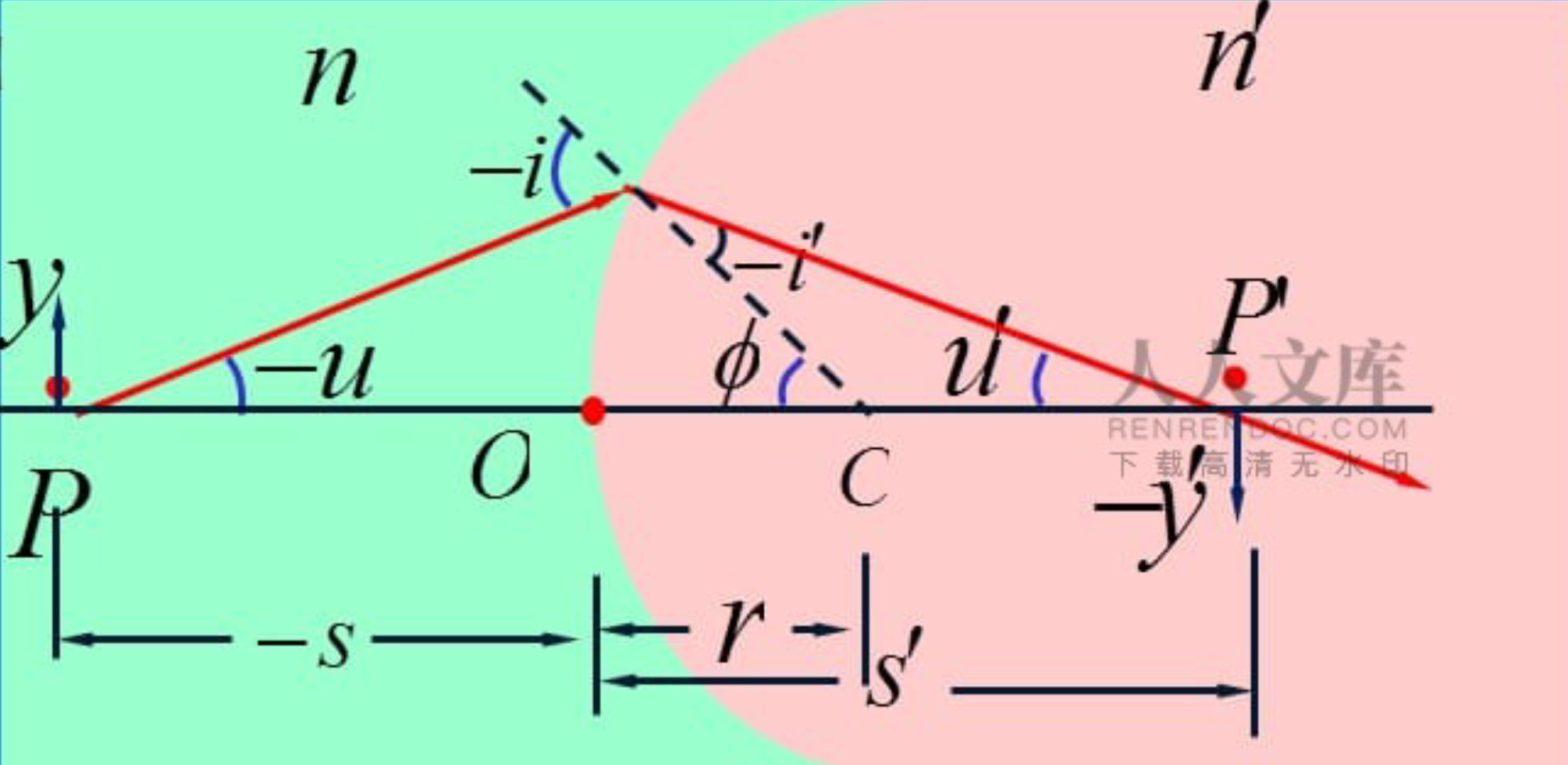傍轴小角度：

\[\sin\theta=\theta，\tan \theta=\theta\]

折射定律：

\[-ni=-n'i'\]

外角关系：

\[-i=-u+\phi，-i'=\phi-u'\]

代入：

\[(n'-n)\phi=n'u'-nu\]

正弦：

\[\phi=\frac{h}{r}，-u=\frac{h}{-s}，u'=\frac{h}{s'}\]

代入得：

\[\boxed{ \frac{n'}{s'}-\frac{n}{s}=\frac{n'-n}{r}=\Phi }\]

光焦度

光学系统固有特征，表示聚光本领。单位：屈光度($D$)，即 $m^{-1}$。

\[\Phi=\frac{n'-n}{r}\]

$\Phi >0$	$\Phi <0$
汇聚作用	发散作用

• 多个紧挨折射面系统的光焦度，是各折射面光焦度之和：

\[\Phi=\Sigma \Phi_{i}\]

解决薄透镜问题。

焦距

• 物方焦距，令 $s’=+\infty$：

\[f=-\frac{n}{n'-n}r=-\frac{n}{\Phi}\]

• 像方焦距，令 $s=-\infty$： \(f'=\frac{n'}{n'-n}r=\frac{n'}{\Phi}\)

高斯成像公式

\[\frac{f'}{s'}+\frac{f}{s}=1\]

推导：阿贝不变式左右同除其右式。

横向放大率

\[\beta=\frac{y'}{y}=\frac{s'}{n'}/\frac{s}{n}=\frac{ns'}{n's}\]

$|\beta|>1$	$|\beta|<1$	$|\beta|=1$
放大像	缩小像	物像等大

$\beta>0$	$\beta<0$
像正立	像倒立
物像在球面同侧	物像在球面异侧
实物成虚像 或 虚物成实像	实物成实像 或 虚物成虚像

纵向放大率

描述物像位置变化相对快慢。

\[\alpha=\frac{ds'}{ds}=\beta^{2} \frac{n'}{n}=\frac{s'^{2}}{n'}/ \frac{s^{2}}{n}=\frac{ns'^{2}}{n's^{2}}>0\]

角放大率

\[\gamma=\frac{\tan u'}{\tan u}=\frac{u'}{u}=\frac{s}{s'}\]

三个放大率关系

横向放大率 $\beta$，纵向放大率 $\alpha$，角放大率 $\gamma$有如下关系：

\[\beta=\alpha \cdot \gamma\]

亥姆霍兹-拉格朗日定理

由角放大率 $\gamma$ 和横向放大率 $\beta$，得：

\[n'y'u'=nyu\]

可推广至多次成像：

\[n_{1}y_{1}u_{1}=n_{1}'y_{1}'u_{1}'=n_{2}y_{2}u_{2}=n_{2}'y_{2}'u_{2}'=n_{k}'y_{k}'u_{k}'\]

球面镜反射

令$n’=-n$，可得球面镜反射的一系列公式。

\[\frac{1}{s'}+\frac{1}{s}=\frac{2}{r}=\frac{1}{f}=\frac{1}{f'}\] \[f=f'=\frac{r}{2}\]

高斯成像公式显然仍成立。

逐次成像法

前一个折射面的像作为后一个折射面的物，逐次代入公式计算。