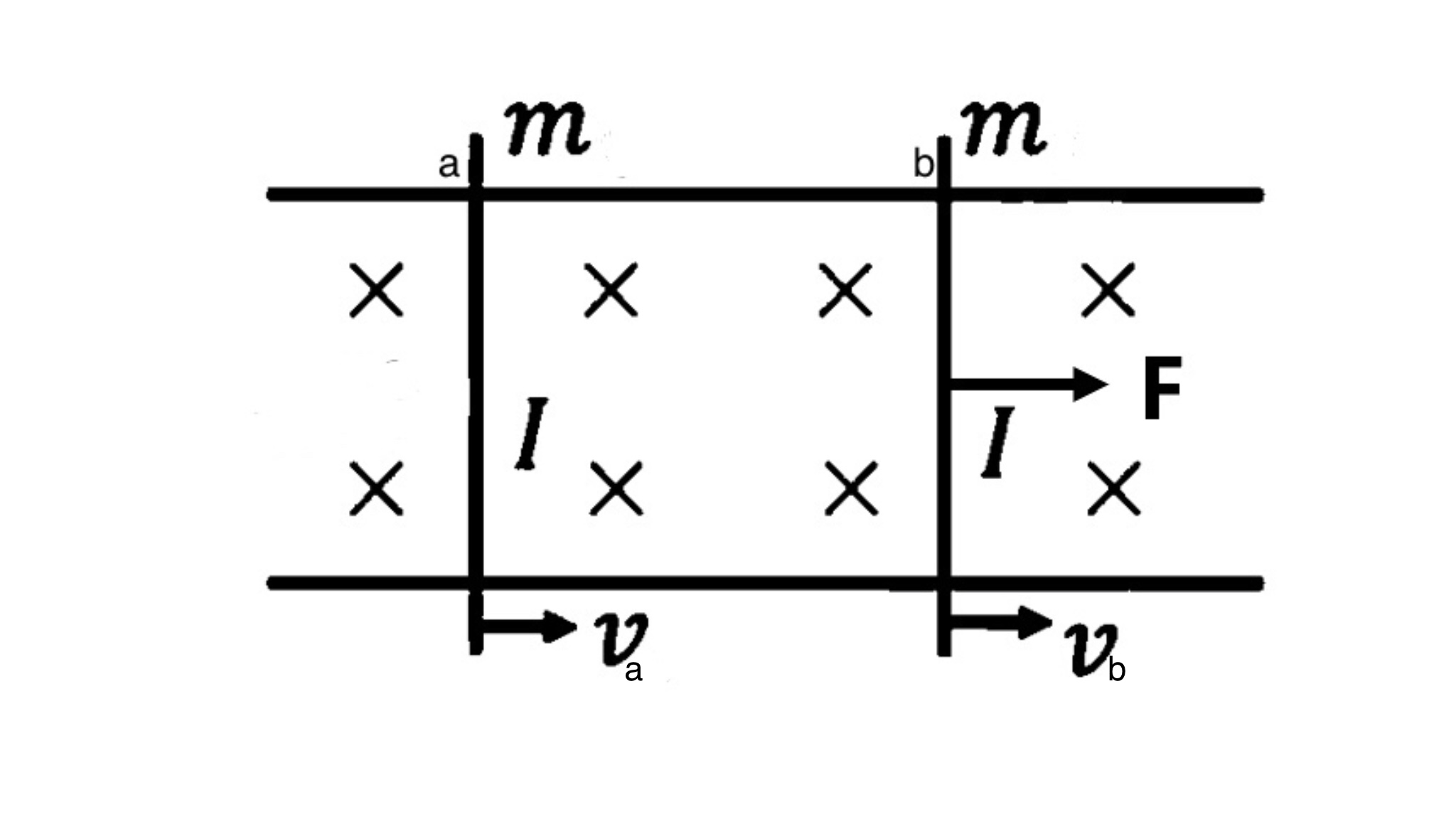
题目
两光滑无限长导电轨道间距为$L$,置于垂直于两导轨的无限大磁场中,磁感应强度为$B$,相同导体棒$a$、$b$垂直放置在导轨上且$a$在$b$左侧,电阻均为$R$,质量均为$m$,初始时均静止。现给$b$施加恒力$F$方向向右,试求两导体棒$v(t)$。
解
导体棒运动切割磁感线产生动生电动势 $\epsilon = BvL$,回路中电流:
\[I=\frac{\epsilon_{b}-\epsilon_{a}}{2R}=\frac{BL(v_b-v_a)}{2R}\]单个导体棒受到安培力:
\[F_安=BIL=\frac{B^2 L^2(v_b-v_a)}{2R}\]列出两导体棒动力学方程:
\[\left\{\begin{matrix} a:m\frac{\mathrm{d} v_a}{\mathrm{d} t}=\frac{B^2 L^2(v_b-v_a)}{2R} \\ b:m\frac{\mathrm{d} v_b}{\mathrm{d} t}=F-\frac{B^2 L^2(v_b-v_a)}{2R} \end{matrix}\right.\]两式作差并整理:
\[\frac{\mathrm{d}}{\mathrm{d} t} (v_b-v_a)+\frac{B^2 L^2} {mR}(v_b-v_a)=\frac F m \tag {*}\]这是一个一阶非齐次线性微分方程。对于一般形式:
\[\frac{dy}{dx}+P(x)y=Q(x)\]有通解:
\[y=e^{-\int{P(x)dx}}\left[ \int{Q(x)e^{\int{P(x)dx}}dx}+C \right]\]则$*$式的解为:
\[v_b-v_a=\frac{RF}{B^2 L^2}(1-e^{-\frac{B^2 L^2 t}{mR}})\tag{1}\]根据动量定理:
\[\begin{align} Ft=mv_a+mv_b\\ v_a+v_b=\frac{Ft} m\tag{2} \end{align}\]联立$1$式、$2$式,解得:
\[\left\{\begin{matrix} v_a=\frac{Ft}{2m}-\frac{RF}{2B^2L^2}(1-e^{-\frac{B^2 L^2 t}{mR}})\\ v_b=\frac{Ft}{2m}+\frac{RF}{2B^2L^2}(1-e^{-\frac{B^2 L^2 t}{mR}}) \end{matrix}\right.\]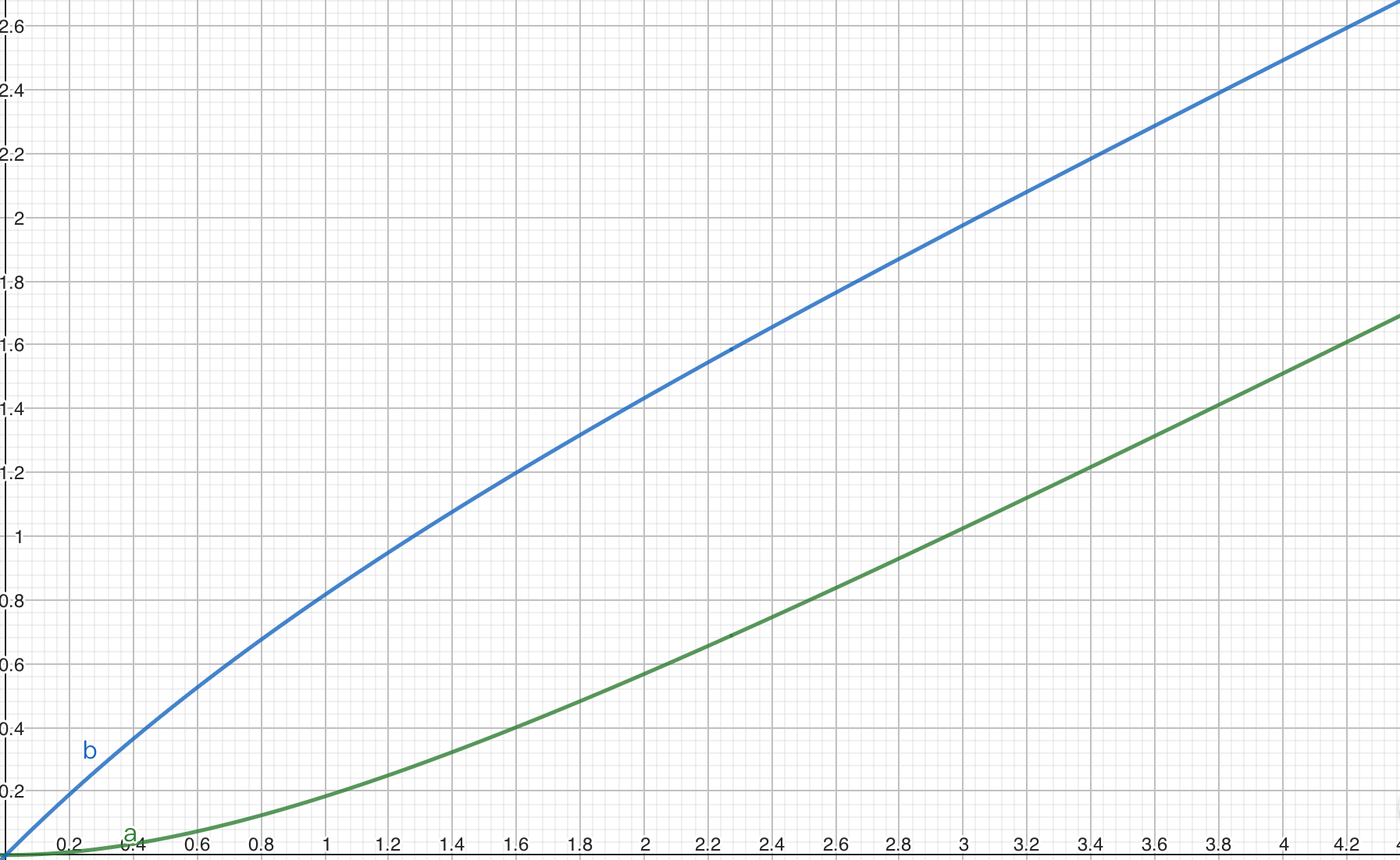
分析
高中课内讲这题,也许会讲:两导体棒先变加速,后匀加速。观察发现,当$t$很大时,$v$的第二项确实几乎不发生变化,加速度接近定值$\frac{F}{2m}$。所以一定程度上可认为导体棒最终近似做匀加速直线运动。