题目
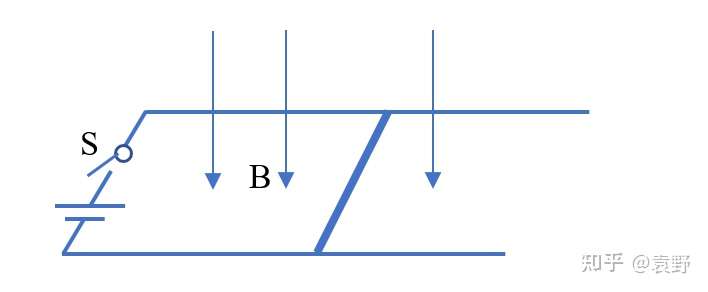
磁感应强度$B$方向竖直,光滑平行导轨间距$L$置于水平面,连接电动势为$\epsilon$内阻为$r$的电源,垂直导轨放置一根电阻为R的导体棒,初速度为0。试求$v(t)$。
解
列出 基尔霍夫回路电压方程(1) 和 动力学方程(2):
\[\left\{ \begin{align} &\epsilon=BLv+I(R+r) \tag{1} \\ &m\frac{\mathrm{d}v}{\mathrm{d}t}=BIL\tag{2} \end{align} \right.\]由(1)得:
\[I=\frac{\epsilon-BLv}{R+r}\]代入(2)并整理:
\[\frac{\mathrm{d}v}{\mathrm{d}t}+\frac{B^2L^2}{m(R+r)}v=\frac{BL\epsilon}{m(R+r)}\]解得:
\[v=\frac{\epsilon}{BL}(1-e^{-\frac{B^2L^2t}{m(R+r)}})\]一阶非齐次线性微分方程的通解参见匀磁场中双杆恒力模型
分析
观察发现,导体棒始终不会匀速运动,只不过当时间极长时,e指数项不断接近0,近似是匀速运动。
吐槽
有些拿此模型出题的老师会给出达到匀速时的位移$x$和过程中产生的焦耳热$Q$,求过程中流过导体棒电荷量。可惜利用动量定理算出的结果与能量守恒算出的结果相差甚远,原因是同时给出$x$与$Q$两个条件,多余,而且$x$与$Q$不对应同一时刻,自相矛盾。
拓展
该模型可将电源换为电容、电阻、电感,又是很有意思的题。