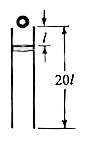
(2023•全国乙卷)如图,一竖直固定的长直圆管内有一质量为$M$的静止薄圆盘,圆盘与管的上端口距离为$l$,圆管长度为$20l$。一质量为$m=\frac{1}{3}M$的小球从管的上端口由静止下落,并撞在圆盘中心,圆盘向下滑动,所受滑动摩擦力与其所受重力大小相等。小球在管内运动时与管壁不接触,圆盘始终水平,小球与圆盘发生的碰撞均为弹性碰撞且碰撞时间极短。不计空气阻力,重力加速度大小为$g$。求圆盘在管内运动过程中,小球与圆盘碰撞的次数。
以竖直向下为正方向。方便起见,先规定如下标记:
| 下标 $_小$ | 下标 $_大$ | 下标 $_n$ | 上标 $’$ | 无上标 |
|---|---|---|---|---|
| 小球 | 薄圆盘 | 第$n$次碰撞 | 碰后瞬间 | 某些情况指碰前瞬间,某些情况无特殊含义 |
不难得知:
\[\begin{align} v_{1大}'=\frac{\sqrt{ 2gl }}{2} &\qquad v_{1小}'=-\frac{\sqrt{ 2gl }}{2}\\ (\quad v_{2大}'=\sqrt{ gl } &\qquad v_{2小}'=0 \quad)\\ t_{n\rightarrow n+1}&=\frac{2(v_{n大}'-v_{n小}')}{g}\qquad (1)\\ \Delta y_{n\rightarrow n+1}&=v_{n大}'\cdot t_{n\rightarrow n+1}\qquad (2) \end{align}\]下面进行第$n$次碰撞到第$n+1$次碰撞的递推。根据空中运动的$v-t$图不难得出:
\[v_{n+1大}=v_{n大}' \qquad v_{n+1小}=2v_{n大}'-v_{n小}'\]由碰撞公式,或联立能量守恒与动量守很,可得碰撞前后速度关系,然后可得两次碰后速度递推关系:
\[v_{n+1大}'=\frac{v_{n+1大}+v_{n+1小}}{2}=\frac{3v_{n大}'-v_{n小}'}{2}\\ v_{n+1小}'=\frac{3v_{n+1大}-v_{n+1小}}{2}=\frac{v_{n大}'+v_{n小}'}{2}\]之后需要求解通项,常规数列方法不再重复。下面接受矩阵法,把上式写成矩阵形式:
\[\left[\begin{matrix} v_{n+1大}'\\ v_{n+1小}' \end{matrix}\right] = \left[\begin{matrix} \frac{3}{2} & -\frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{matrix}\right] \left[\begin{matrix} v_{n大}'\\ v_{n小}' \end{matrix}\right] \\ \left[\begin{matrix} v_{n大}'\\ v_{n小}' \end{matrix}\right] = \left[\begin{matrix} \frac{3}{2} & -\frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{matrix}\right]^{n-1} \left[\begin{matrix} v_{1大}'\\ v_{1小}' \end{matrix}\right]\]现在需要解决一个二阶方阵的幂。由Sylvester定理可求得下式(虽然我也不会,但我会套公式…):
\[\left[\begin{matrix} A&B\\C&D \end{matrix}\right]^{n} = \frac{1}{\sin \phi}\left[\begin{matrix} A\sin n\phi-\sin(n-1)\phi & B\sin n\phi\\ C\sin n\phi & D\sin n\phi-\sin(n-1)\phi \end{matrix}\right]\\ \phi=\arccos\frac{A+D}{2}\]代入此题数据,发现$\phi=0$,完蛋了,$\frac{0}{0}$。别急,这不有菜刀吗!哦不,我的意思是这不有 洛必达 吗!在菜刀的提示下,我们很流畅地算出:
\[\left[\begin{matrix} v_{1大}'\\ v_{1小}' \end{matrix}\right] = \left[\begin{matrix} \frac{n+1}{2} & \frac{-n+1}{2}\\ \frac{n-1}{2} & \frac{3-n}{2} \end{matrix}\right] \left[\begin{matrix} \frac{\sqrt{ 2gl }}{2}\\ -\frac{\sqrt{ 2gl }}{2} \end{matrix}\right] = \left[\begin{matrix} \frac{\sqrt{ 2gl }}{2}n\\ \frac{\sqrt{ 2gl }}{2}(n-2) \end{matrix}\right]\]代入(1)(2)式,得:
\[t_{n\rightarrow n+1}=\frac{2\sqrt{ 2gl }}{g}\\ \Delta y_{n\rightarrow n+1}=2nl\]不难得出答案:4次。
排版太丑了,但是…就这样能看就行吧